To solve the system of equations, we can use the method of Gaussian elimination. Here are the steps:
Step 1: Write the system of equations in matrix form:
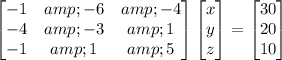
Step 2: Apply row operations to transform the matrix into row-echelon form.
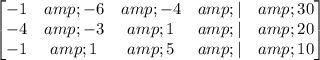
First, we will perform row 2 = row 2 + 4 * row 1 and row 3 = row 3 + row 1.
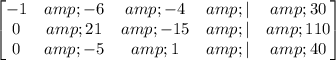
Next, we will perform row 2 = (1/21) * row 2 and row 3 = row 3 + (5/21) * row 2.
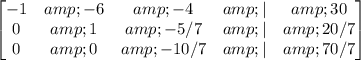
Finally, we will perform row 3 = (7/10) * row 3.
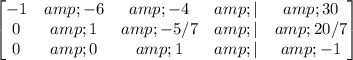
Step 3: Back-substitution
From the row-echelon form, we can read the values of x, y, and z:

Therefore, the solution to the system of equations is:

Please note that the solution is in fractional form. It can be simplified or expressed as a decimal if needed.