the calculation
 shows that
shows that
 must be the cube root of 37 because it is the number that, when raised to the third power, equals 37. This is why
must be the cube root of 37 because it is the number that, when raised to the third power, equals 37. This is why
 is the same as the cube root of 37.
is the same as the cube root of 37.
To explain this concept to your friend who missed class, let's start with the basic exponent rules they would know. One of the fundamental rules of exponents is that when you raise a power to another power, you multiply the exponents. So if we have
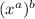 , the result is
, the result is
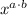 .
.
Now, let's apply this rule to the expression
 :
:
1. We multiply the exponents
 and
and
 together:
together:
![\[ (37^(1/3))^3 = 37^((1/3 \cdot 3)) = 37^1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a7m6v7d0yr537eoteknzw4y8hz7em3dd23.png)
2.
 simply means 37 to the power of 1, which is just 37 itself:
simply means 37 to the power of 1, which is just 37 itself:
![\[ 37^(1) = 37 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/et43q3b11plghe678da05cwkk6hpea37gx.png)
This demonstrates that
 results in the original number, 37. This is because the exponent
results in the original number, 37. This is because the exponent
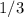 is the reciprocal of 3. When we raise 37 to the
is the reciprocal of 3. When we raise 37 to the
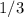 power, we are essentially finding a number that, when multiplied by itself three times (which is what the cube of a number means), gives us 37 back. Therefore,
power, we are essentially finding a number that, when multiplied by itself three times (which is what the cube of a number means), gives us 37 back. Therefore,
 is indeed the cube root of 37, because cubing the cube root of a number returns the original number.
is indeed the cube root of 37, because cubing the cube root of a number returns the original number.
So, the calculation
 shows that
shows that
 must be the cube root of 37 because it is the number that, when raised to the third power, equals 37. This is why
must be the cube root of 37 because it is the number that, when raised to the third power, equals 37. This is why
 is the same as the cube root of 37.
is the same as the cube root of 37.