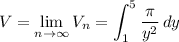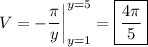Question

Find the volume of the solid formed by rotating the region bounded by the given curves about the indicated axis. Y = 1x, y = 1, y = 5, x = 0; about the y-axis.

Answer 1

The disk method will only involve a single integral. I've attached a sketch of the bounded region (in red) and one such disk made by revolving it around the y-axis.

Such a disk has radius x = 1/y and height/thickness ∆y, so that the volume of one such disk is

π (radius) (height) = π (1/y)² ∆y = π/y² ∆y

and the volume of a stack of n such disks is

`\displaystyle V_n = \sum_(i=1)^n \pi {y_i}^2 \Delta y`

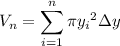
where
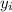`y_i` is a point sampled from the interval [1, 5].

As we refine the solid by adding increasingly more, increasingly thinner disks, so that ∆y converges to 0, the sum converges to a definite integral that gives the exact volume V,

`\displaystyle V = \lim_(n\to\infty) V_n = \int_1^5 (\pi)/(y^2) \, dy`

`V = -\frac\pi y\bigg|_(y=1)^(y=5) = \boxed{\frac{4\pi}5}`