Answer:
C) 318°
Explanation:
Line segment LM appears to be a diameter of the circle.
As angles on a straight line sum to 180°, and an arc measure is equal to its corresponding central angle measure, then the value of x can be calculated as follows:

Therefore, the measure of minor arc JK is:
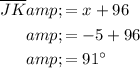
The name of an arc is derived from the points used to define it.
Major arcs (greater than 180°) are always named with three letters: the starting point of the arc, a point on the arc, and the endpoint of the arc.
Therefore, arc JLI is the sum of the minor arcs JK, KL, LM and MI:
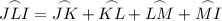
We know that JK = 91° and KL = 47°.
As line segment LI appears to be the diameter, the sum of minor arcs LM and MI is 180°. Therefore:
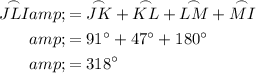
Therefore, the measure of the major arc JLI is 318°.