Question

In PQR, Q= 76, PQ = 18, and QR = 27
Please find angle P, T and PR for 5

Answer 1

Explanation:

Given:

m<Q = 76°

PQ = r = 18

QR = p = 27

Required:

Find P, T, and PR (q)

Solution:

✔️To find PR(q), apply the Law of Cosines.

Thus:

q² = r² + p² - 2rp×cos(Q)

Plug in the values

q² = 18² + 27² - 2×18×27×cos(76)

q² = 1,053 - 235.148

q² = 817.852

q = √817.852

q = 28.6 (nearest tenth)

✔️Find P by applying the Law of Sines:

`(sin(P))/(p) = (sin(Q))/(q)`

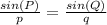
Plug in the values

`(sin(P))/(27) = (sin(76))/(28.6)`

`sin(P) = (sin(76)*27)/(28.6)`

`sin(P) = 0.9160`

`P = sin^(-1)(0.9160)`

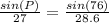
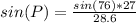
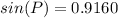
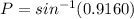
P = 66.3° (nearest tenth)

✔️R = 180 - (P + Q)

R = 180 - (66.3 + 76)

R = 37.7°