Answer:
Explanation:
Given:
m<Q = 76°
PQ = r = 18
QR = p = 27
Required:
Find P, T, and PR (q)
Solution:
✔️To find PR(q), apply the Law of Cosines.
Thus:
q² = r² + p² - 2rp×cos(Q)
Plug in the values
q² = 18² + 27² - 2×18×27×cos(76)
q² = 1,053 - 235.148
q² = 817.852
q = √817.852
q = 28.6 (nearest tenth)
✔️Find P by applying the Law of Sines:

Plug in the values
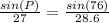

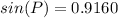
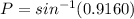
P = 66.3° (nearest tenth)
✔️R = 180 - (P + Q)
R = 180 - (66.3 + 76)
R = 37.7°