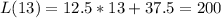Answer:
L(13) = 200
Explanation:
Linear function:
A linear function has the following format:

In which m is the slope(how much y changes when x changes by 1) and b is the y-intercept(value of y when x = 0).
Finding the slope:
L (5) = 100 and L (9) = 150.
The slope is given by the change in the output(L, which is equals to y in the general formula) divided by the change in the input(x).
Change in the output: 150 - 100 = 50
Change in the input: 9 - 5 = 4
Slope:

So
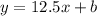
L (5) = 100
So
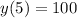 , which means that when
, which means that when
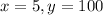 , and we use this to find b.
, and we use this to find b.
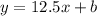
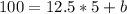
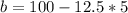
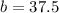
So
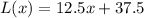
a. Determine the value of L (13)
L when
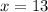 . So
. So