Question

Suppose the function y=y(x) solves the initial value problem

dy/dx=2y/1+x^2
y(0)=2
find y(2)

Answer 1

`y(2)=2e^{2\tan^(-1)(2)}`

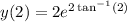
Explanation:

Given the initial value problem.

`(dy)/(dx)=(2y)/(1+x^2) ; \ y(0)=2`

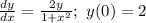
Find y(2)

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`\boxed{\left\begin{array}{ccc}\text{\underline{Seperable Differential Equation:}}\\(dy)/(dx) =f(x)g(y)\\\\\rightarrow\int(dy)/(g(y))=\int f(x)dx \end{array}\right }`

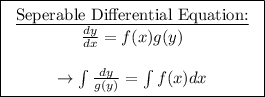
(1) - Solving the separable DE

`(dy)/(dx)=(2y)/(1+x^2) \\\\\Longrightarrow (1)/(y)dy =(2)/(1+x^2)dx\\ \\\Longrightarrow \int (1)/(y)dy =2 \int(1)/(1+x^2)dx\\\\\Longrightarrow \boxed{ \ln(y)=2\tan^(-1)(x)+C}`

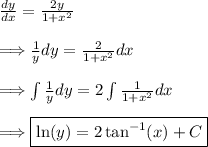
(2) - Find the arbitrary constant "C" with the initial condition

`\text{Recall} \rightarrow y(0)=2\\ \\ \ln(y)=2\tan^(-1)(x)+C\\\\\Longrightarrow \ln(2)=2\tan^(-1)(0)+C\\\\\Longrightarrow \ln(2)=0+C\\\\\therefore \boxed{C=\ln(2)}`

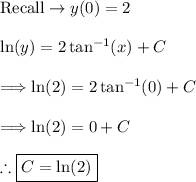
(3) - Form the solution

`\boxed{\boxed{ \ln(y)=2\tan^(-1)(x)+\ln(2)}}`

(4) - Solve for y

`\ln(y)=2\tan^(-1)(x)+\ln(2)\\\\ \Longrightarrow \ln(y)-\ln(2)=2\tan^(-1)(x)\\\\ \Longrightarrow \ln((y)/(2) )=2\tan^(-1)(x)\\\\ \Longrightarrow e^{\ln((y)/(2) )}=e^{2\tan^(-1)(x)}\\\\ \Longrightarrow (y)/(2) =e^{2\tan^(-1)(x)}\\\\\therefore \boxed{y=2e^{2\tan^(-1)(x)}}`

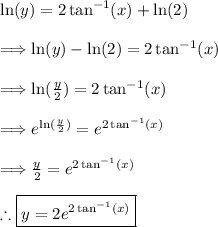
(5) - Find y(2)

`y=2e^{2\tan^(-1)(x)}\\\\\therefore \boxed{\boxed{y(2)=2e^{2\tan^(-1)(2)}}}`

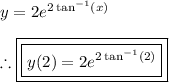
Thus, the problem is solved.