Answer:
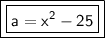
Explanation:
The area of a rectangle is the product of length and width.
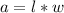
The length is (x+5) and the width is (x-5).
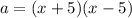
We have two binominals, so we can multiply using FOIL: First, Outside, Inside, Last.
- F: x*x= x²
- O: x*-5= -5x
- I: x*5= 5x
- L: 5*-5 = -25
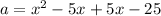
Combine the like terms: -5x and 5x. They cancel each other out.
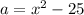
The area of the rectangle is x²-25