Question

What is the area of the rectangle whose length is (x + 5) and width (x-5)​

Answer 1

area of the rectangle is length *breadth

length =(x+5)

breadth =(x-5)

=(x+5)(x-5)=x^2-5x+5x-25=x^2-25

Answer 2

`\boxed {\boxed {\sf a=x^2-25}}`

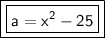
Explanation:

The area of a rectangle is the product of length and width.

`a=l*w`

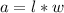
The length is (x+5) and the width is (x-5).

`a= (x+5)(x-5)`

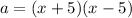
We have two binominals, so we can multiply using FOIL: First, Outside, Inside, Last.

• F: x*x= x²
• O: x*-5= -5x
• I: x*5= 5x
• L: 5*-5 = -25

`a= x^2-5x+5x-25`

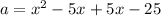
Combine the like terms: -5x and 5x. They cancel each other out.

`a=x^2-25`

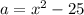
The area of the rectangle is x²-25