Answer:
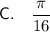
Explanation:
To find the area under the curve of a function f(x) between specified limits, we can use definite integration.
Definite integration
The definite integral of f(x) with respect to x between the limits x = a and x = b is:
![\boxed{\displaystyle \int^b_a \text{f}(x)\; \text{d}x=\left[\text{g}(x)\right]^b_a=\text{g}(b)-\text{g}(a)}](https://img.qammunity.org/2024/formulas/mathematics/college/9wcnl2ql74u06dn7y5xv58def5wwnbszwv.png)
where a is the lower limit and b is the upper limit.
Given function:
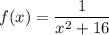
First we need to determine if the function f(x) crosses the x-axis between the given limits of x = 0 and x = 4. (If any part of the curve between these limits is below the x-axis, we will need to integrate each part separately).
A function crosses the x-axis when y = 0. As the function is a rational function where the denominator is greater than or equal to 16, then y > 0. Therefore, the curve is always above the x-axis, and is continuous between the given limits.
Therefore, the definite integral to evaluate is:
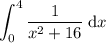
To evaluate the integral, use the method of substitution.
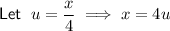
Differentiate u with respect to x to find du/dx:
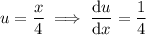
Rearrange to isolate dx:
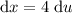
Use the substitution to change the limits of the integral from x-values to u-values:
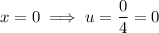
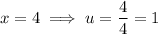
As x = 4u, then function f(u) is:

Substitute everything back into the original integral to create a definite integral in terms of u:
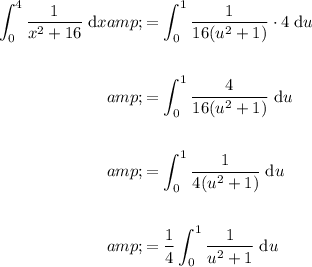
Use the following integration formula to evaluate the integral:

Therefore:
![\begin{aligned}\displaystyle \int^4_0 (1)/(x^2+16)\; \text{d}x&=(1)/(4)\int^1_0 (1)/(u^2+1) \;\text{d}u\\\\&=(1)/(4)\left[\vphantom{\frac12}\arctan u\right]^1_0\\\\&=(1)/(4)\arctan (1)-(1)/(4) \arctan(0)\\\\&=(1)/(4)\cdot (\pi)/(4)-(1)/(4) \cdot 0\\\\&=(\pi)/(16)\end{aligned}](https://img.qammunity.org/2024/formulas/mathematics/college/kf7zibge4dmjs9c61z4z7r9fgzrh0bif82.png)
So the area under the curve of the function f(x) between the limits 0 and 4 is π/16.