Answer:
The value of the Golden Igloo is $227.4 million.
Step-by-step explanation:
First, we need to find the inner and the outer volume of the half-spherical shell:
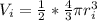
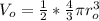
The total volume is given by:
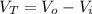
Where:
 : is the inner volume
: is the inner volume
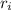 : is the inner radius = 1.25/2 = 0.625 m
: is the inner radius = 1.25/2 = 0.625 m
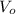 : is the outer volume
: is the outer volume
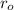 : is the outer radius = 1.45/2 = 0.725 m
: is the outer radius = 1.45/2 = 0.725 m
Then, the total volume of the Igloo is:
![V_(T) = (2)/(3)\pi r_(o)^(3) - (2)/(3)\pi r_(i)^(3) = (2)/(3)\pi [(0.725 m)^(3) - (0.625 m)^(3)] = 0.29 m^(3)](https://img.qammunity.org/2022/formulas/chemistry/high-school/7p11szyd4o3oqrh6ymilifxe2xplzzbuo1.png)
Now, by using the density we can find the mass of the Igloo:

Finally, the value (V) of the antiquity is:
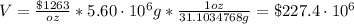
Therefore, the value of the Golden Igloo is $227.4 million.
I hope it helps you!