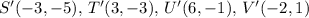 .
.
To find the images of the vertices S, T, U, and V of Quadrilateral STUV after a reflection across the line
 , we can use the formula for reflecting a point
, we can use the formula for reflecting a point
 across a horizontal line
across a horizontal line
 :
:
![\[ (x, y) \rightarrow (x, 2k - y) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1d5g5lqbfh7pobvw7azwkmxqfeisds0kvb.png)
In this case, the line of reflection is
 , so the formula becomes:
, so the formula becomes:
![\[ (x, y) \rightarrow (x, -8 - y) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6d08liytq4jtq6w3s5r8wncmr3udcynh1r.png)
Now, apply this formula to each vertex:
1. S' ( _, _ )
For S(-3, -3):
![\[ S'(-3, -8 - (-3)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u06yzcz70iw0ty8t58ki1dd0dzgwbwl6hg.png)
![\[ S'(-3, -5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4yl3ndi6bqn78ny9b9bvcd50v7jfttwlf8.png)
2. T' ( _, _ )
For T(3, -5):
![\[ T'(3, -8 - (-5)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mopmakj3a8ukfo5h0ukq5ft590cvz1kypf.png)
![\[ T'(3, -3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f78r4u5lvepjekne922vm3moj9tvk1dvdm.png)
3. U' ( _, _ )
For U(6, -7):
![\[ U'(6, -8 - (-7)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/izjqspuo7i9d08p0a6mhdsmpl1vu46cv7o.png)
![\[ U'(6, -1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fhfz3uc34cp0qqs45xkpjtmxje8sf6qhex.png)
4. V' ( _, _ )
For V(-2, -7):
![\[ V'(-2, -8 - (-7)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/iqm7vc1jj5848nh1liy2dv50xsx1c01yz0.png)
![\[ V'(-2, 1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/brk5ji7rfcr22eb9emhsnkckhcv2xj2uth.png)
Therefore, the images of the vertices after the reflection are:
![\[ S'(-3, -5), \, T'(3, -3), \, U'(6, -1), \, V'(-2, 1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bzqixksrfo9vxu4lpbp3h2xet4qremg496.png)