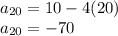Answer:
3. 255
4. -70
Explanation:
3.
For the arithmetic sequence 8, 21, 34, 47, 60, ...
The common difference between consecutive terms is d =(21-8)= 13. Therefore, the nth term of the sequence can be expressed as:
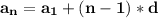
where
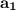 is the first term of the sequence,
is the first term of the sequence,
n is the term number, and d is the common difference.
Substituting
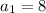 and d = 13, we get:
and d = 13, we get:
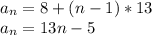
To find
 , substitute n = 20 in the above formula:
, substitute n = 20 in the above formula:
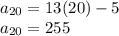
4.
For the arithmetic sequence 6, 2, -2, -6, -10, ...
The common difference between consecutive terms is d =(2-6)= -4. Therefore, the nth term of the sequence can be expressed as:
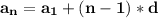
where
 is the first term of the sequence,
is the first term of the sequence,
n is the term number, and
d is a common difference.
Substituting
 = 6 and d = -4, we get:
= 6 and d = -4, we get:
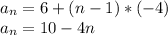
To find
 , substitute n = 20 in the above formula:
, substitute n = 20 in the above formula: