Answer:
The coordinates of the intersection of the diagonal of the parallelogram are
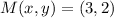 .
.
Explanation:
Diagonals are represented by line segments GJ and KH. Since quadrilateral is a parallelogram, then coordinates of the intersection are located at midpoint of each diagonal (
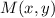 ). That is:
). That is:

![M(x,y) = G(x,y) +(1)/(2)\cdot [J(x,y)-G(x,y)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/9orr49vfdejglkapdvp49j7w3sa42fhp31.png) (1)
(1)
If we know that
 and
and
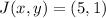 , the coordinates of the intersection of the diagonals of the parallelogram are:
, the coordinates of the intersection of the diagonals of the parallelogram are:
![M(x,y) = (1,3) +(1)/(2)\cdot [(5,1)-(1,3)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/az5q91lu4ox7rt08nalmsqikjtob5a96l6.png)
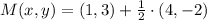
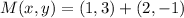
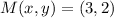
There is another form:
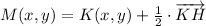
![M(x,y) = K(x,y) + (1)/(2)\cdot [H(x,y)-K(x,y)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ia5d659uwod7xmq3sbatupkzctkmxka3ds.png) (2)
(2)
If we know that
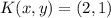 and
and
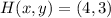 , the coordinates of the intersection of the diagonals of the parallelogram are:
, the coordinates of the intersection of the diagonals of the parallelogram are:
![M(x,y) = (2,1) + (1)/(2)\cdot [(4,3)-(2,1)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/279txunvsltf9bhzi07djnco2pf4wxn3bc.png)
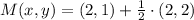
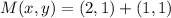
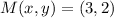
Therefore, the coordinates of the intersection of the diagonal of the parallelogram are
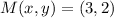 .
.