Answer: 7.635 square meters
Explanation:
Both triangles have the diameter as one of their sides and they both have a vertex on the circumference of the circle. Thus, the two triangles are right triangles, and the hypotenuse of the triangles is the diameter.
Use the Pythagorean Theorem:
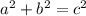
Square root both sides to isolate c (hypotenuse/diameter):

Plug in the values of a and b to calculate c:
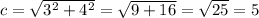
The diameter of the circle is 5 meters, so the radius of the circle is 2.5 meters.
Plug in the radius into the equation for the area of a circle: Area =
 square meters.
square meters.
The equation for the area of a triangle is
 , where b is the base of the triangle and h is the height of the triangle.
, where b is the base of the triangle and h is the height of the triangle.
Since we have two congruent triangles, the total area of the two triangles combined is simply b*h.
Plug in the values of b and h to get b*h = 3*4 = 12 square meters.
Subtract the total area of the two triangles combined from the area of the circle to get the area of the shaded region:
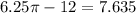 square meters.
square meters.