Question

Find the value of x in the figure. Figure is not drawn to scale.

Answer 1

x=105

Explanation:

Two methods

Method 1. Solving with Exterior Angles

Method 2. Solving with Interior Angles

Method 1. Solving with Exterior Angles

So that we can keep things organized, let's call the angle in the bottom left of the triangle, Angle 1, the angle in the top of the triangle, Angle 2, and the angle in the bottom right of the triangle, Angle 3.

An Exterior Angle is formed by continuing the line segment of a side, and is the angle that forms a linear pair with the interior angle.

Observe that all of the angles given are Exterior Angles to the Polygon (in this case, a triangle), and only one exterior angle is given for each vertex (we don't want to double-count things).

For any polygon, the sum of its exterior angles is always 360 degrees.

Therefore, we can setup the following equation:

`360^o=m \angle 1_(exterior) + m \angle 2_(exterior) + m \angle 3_(exterior)`

`360^o=(145^o) + (110^o) + (x^o)`

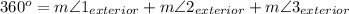
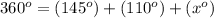
Combining like terms on the right hand side...

`360^o=x^o +255^o`

Isolating x by subtraction 255 degrees from both sides...

`(360^o)-255^o=(x^o +255^o)-255^o`

`105^o=x^o`

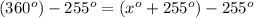
So, x = 105

Method 2. Solving with Interior Angles

An Interior Angle is the angle we usually think of inside of a polygon (in this case, a triangle).

The sum of the Interior angles of any polygon is given by
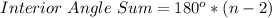`Interior~Angle~Sum=180^o*(n-2)`, where "n" is the number of sides of the polygon. For triangles, n=3, so

`Interior~Angle~Sum=180^o*((3)-2)`

`Interior~Angle~Sum=180^o*(1)`

`Interior~Angle~Sum=180^o`

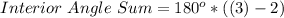
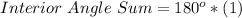
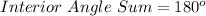
In this case, we're given exterior angles for two of the vertices, and we've been asked to find the exterior angle for the third vertex. Each Exterior angle forms a linear pair with the interior angle, and thus is supplementary, meaning a pair of Interior and Exterior angles have measures that add to 180 degrees.

Keeping with our angle numbering described in Method 1, we have the following 3 true equations about each interior/exterior pair, where we can substitute in the known values, and solve for / isolate the unknown angle measure (in the last case, we'll get an expression containing "x" for its measure):

`\begin{array}{ccc}180^o=m \angle 1+m \angle 1_(exterior)&180^o=m \angle 2+m \angle 2_(exterior)&180^o=m \angle 3+m \angle 3_(exterior)\\180^o=m \angle 1+(145^o)&180^o=m \angle 2+(110^o)&180^o=m \angle 3+(x^o)\\180^o-145^o=m \angle 1&180^o-110^o=m \angle 2&180^o-(x^o)=m \angle 3\\35^o=m \angle 1&70^o=m \angle 2&180^o-(x^o)=m \angle 3\end{array}`

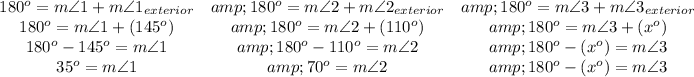
Additionally, since the sum of the interior angles of a triangle is 180 degrees, we also have the following equation...

`m \angle 1 + m \angle 2 + m \angle 3 = 180^o`

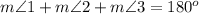
Making substitutions with the quantities found above...

`(35^o) + (70^o) + (180^o-x^o) = 180^o`

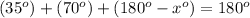
Rewriting subtraction as addition of a negative...

`35^o + 70^o + 180^o + (-x^o) = 180^o`

Adding x degrees to both sides, and subtracting 180 degrees from both sides...

`35^o + 70^o =x^o`

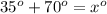
Combining like terms..

`105^o =x^o`

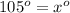
So, again, x=105

Answer 2

`x^(0) =105^(0)`

Explanation:

`x^(0) =180-(180-(180-110)-(180-145))`

`x^(0) =180-(180-70-35)`

`x^(0) =180-75`

`x^(0) =105`

Hope this helps