Question

A bag contains tiles number 1-10. What is the probability of first selecting a PRIME number, replacing it, then selecting a number less than or equal to 3?​

Answer 1

0.12 = 12% probability of first selecting a PRIME number, replacing it, then selecting a number less than or equal to 3

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

Probability of independent events:

Suppose we have two events, A and B, that are independent. The probability of both happening is given by:

`P(A \cap B) = P(A) * P(B)`

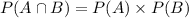
In this question:

Event A: Selecting a prime number.

Event B: Selecting a number less than or equal to 3

Probability of selecting a prime number:

Between 1 and 10, we have 4 prime numbers(2,3, 5 and 7), out of 10. So

`P(A) = (4)/(10)`

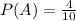
Probability of selecting a number less than or equal to 3:

Three numbers(1,2,3) out of 10. So

`P(B) = (3)/(10)`

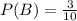
Probability of both:

`P(A \cap B) = P(A) * P(B) = (4)/(10) * (3)/(10) = (12)/(100) = 0.12`

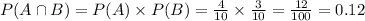
0.12 = 12% probability of first selecting a PRIME number, replacing it, then selecting a number less than or equal to 3