C. 960 sq in.
To find the surface area of the hexagonal prism, we need to find the areas of all the surfaces and then add them up.
Hexagonal Bases:
Each hexagonal base has an area given by the formula:
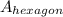 =
=
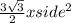 =
=
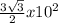
Lateral Faces (Rectangles):
There are six rectangular lateral faces. Each rectangle's area is given by
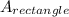 =length×width = 6×(10×7).
=length×width = 6×(10×7).
Triangles on the Sides:
There are six identical triangles on the sides. Each triangle's area is given by
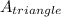 =
=
 ×base×height = 6 x
×base×height = 6 x
 x 10 x 9
x 10 x 9
Now, let's calculate these areas and add these areas to get the total surface area
Total Surface Area ≈960sq in