Question

A river flows with a uniform velocity vr. A person in a motorboat travels 1.22 km upstream, at which time she passes a log floating by. Always with the same engine throttle setting, the boater continues to travel upstream for another 1.45 km, which takes her 69.1 min. She then turns the boat around and returns downstream to her starting point, which she reaches at the same time as the same log does. How much time does the boater spend traveling back downstream

Answer 1

t ’=
`(1450)/(0.6499 + 2 v_r)`, v_r = 1 m/s t ’= 547.19 s

Step-by-step explanation:

This is a relative velocity exercise in a dimesion, since the river and the boat are going in the same direction.

By the time the boat goes up the river

v_b - v_r = d / t

By the time the boat goes down the river

v_b + v_r = d '/ t'

let's subtract the equations

2 v_r = d ’/ t’ - d / t

d ’/ t’ = 2v_r + d / t

`t' = (d')/( (d)/(t)+ 2 v_r )`

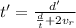
In the exercise they tell us

d = 1.22 +1.45 = 2.67 km= 2.67 10³ m

d ’= 1.45 km= 1.45 1.³ m

at time t = 69.1 min (60 s / 1min) = 4146 s

the speed of river is v_r

t ’=
`(1.45 \ 10^3)/( ( 2670)/(4146) \ + 2 \ v_r)`

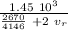
t ’=
`(1450)/(0.6499 + 2 v_r)`

In order to complete the calculation, we must assume a river speed

v_r = 1 m / s

let's calculate

t ’=
`( 1450)/( 0.6499 + 2 \ 1)`

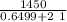
t ’= 547.19 s