Question

a 45-cm -long, 65 g rod rotates about an axle at one end of the rod. at what angular velocity, in rpm , does the rod have 50 mj of rotational kinetic energy?

Answer 1

The angular velocity of the rod is 45.6 rpm (4.78 rad/s).

Given:

Length of the rod (L) = 45 cm = 0.45 m

Mass of the rod (m) = 65 g = 0.065 kg

Rotational kinetic energy (K) = 50 mJ = 50 x
`10^(-3)` J

Rotational kinetic energy is given by the formula:

K =
`(1)/(2) I`ω²

where I is the moment of inertia of the rod and ω is the angular velocity.

For a uniform rod rotating about one end, the moment of inertia is given by:

I =
`(1)/(3)ML^(2)` =
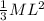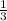`(1)/(3)` x 0.065 x 0.45 x 0.45

Substituting the given values:

K =
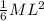`(1)/(6) ML^(2)`ω²

Solving for ω:

ω =
`\sqrt{(6K)/(ML^(2)) }` =
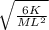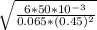`\sqrt{(6 * 50 *10^(-3))/(0.065*(0.45)^(2)) }` = 4.78 rad/s

To convert to rpm:

1 rad/s = 9.54 rpm

4.78 rad/s = 4.78 x 9.54 = 45.6 rpm

This is the angular velocity of the given rod.

Answer 2

The angular velocity of the rod is determined as 4.77 rad/s.

How to calculate the angular velocity?

The angular velocity of the rod is calculated by applying the following formula as shown below;

K.E = ¹/₂Iω²

where;

• I is the moment of inertia
• ω is the angular velocity

The formula for the moment of inertia of the rod is;

I = ¹/₃ML²

K.E = ¹/₂(¹/₃ML²)ω²

K.E = ¹/₆ML²ω²

ω² = 6K.E / ML²

ω = √ (6K.E / ML²)

The angular velocity of the rod is calculated as;

ω = √ (6 x 0.05 / (0.065 x 0.45²))

ω = 4.77 rad/s