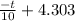Question

A tank contains 10 liters of pure water. A solution of an unknown, but constant concentration of salt is flowing in at 0.5 liters per minute. The water is mixed well and drained at 1 liter per minute. After 20 minutes there are 10 grams of salt in the tank. (i) Give an adequate mathematical model for this scenario. Explain what each of your variables means. (ii) What is the concentration of the incoming salt solution

Answer 1

i) ∴∫
`(dA)/(A)` = ∫
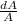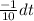`(-1)/(10) dt` ------ ( 1 )

ii) C = 4.303

Step-by-step explanation:

Given data:

water in tank = 10 liters

concentration of salt flowing in = 0.5 liters/min

10 grams of salt is left in tank after 20 minutes

mixed water is drained at 1 liter per minute

i) Adequate mathematical model for the scenario

lets assume ; A( t ) amount of salt after t minute

A( t ) = 10grams where t = 20 minutes

differentiate A(t)

dA / dt = ( rate in ) - ( rate out )

= 0.5 * 0 - A/10

∴∫
`(dA)/(A)` = ∫
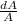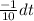`(-1)/(10) dt` ------ ( 1 )

ii) hence; In A =
`(-1)/(10) t + C` ----- ( 2 )

at t = 20 , A = 10grams

find C = In 10 + 2

= 2.303 + 2 = 4.303

back to ( 2 )

In A =
`(-t)/(10) + 4.303`

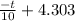
∴ A = e
`(-t)/(10) + 4.303`