Answer:
5.0 inches
Explanation:
The formula for the volume of a sphere is:

where r is the radius of the sphere.
Given a sphere has a volume of 65.5 cubic inches, substitute V = 65.5 into the formula and solve for the radius, r:
![\begin{aligned}\implies (4)/(3)\pi r^3&=65.5\\\\3 \cdot (4)/(3)\pi r^3&=3 \cdot 65.5\\\\4\pi r^3&=196.5\\\\(4\pi r^3)/(4 \pi)&=(196.5)/(4 \pi)\\\\r^3&=15.636973...\\\\\sqrt[3]{r^3}&=\sqrt[3]{15.636973...}\\\\r&=2.50063840...\; \sf in\end{aligned}](https://img.qammunity.org/2024/formulas/mathematics/high-school/qgmd2gxm7pa4m30q476y2n73uzpf7aq1l8.png)
The diameter of a sphere is twice its radius.
Therefore, if the radius is 2.50063840... inches, then the diameter is:
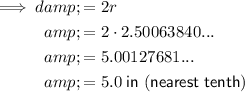
Therefore, the diameter of a sphere with a volume of 65.5 cubic inches is 5.0 inches, to the nearest tenth of an inch.