Question

An arithmetic sequence begins with −20, −16, −12, −8, −4 …

Which option below represents the formula for the sequence?

f(n) = −20 − 4(n−1)
f(n) = −20 + 4(n−1)
f(n) = −20 − 4(n+1)
f(n) = −20 + 4(n+1)

Answer 1

f(n) = -20 + 4(n - 1)

Explanation:

The explicit formula for an arithmetic sequence in function notation is
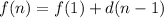`f(n) = f(1) + d(n - 1)`, where:

• 
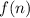  `f(n)` = any number
• 
  `f(1)` = first term
• 
  `d` = common difference
• 
  `(n - 1)` = one less than the term number

We need to find the values of f(1) (the first term) and 'd' (the common difference). The first term in the arithmetic sequence is -20 because it's the beginning number. The common difference is 4 because we add 4 to each term to get the next term (-20 + 4 = -16, -16 + 4 = -12, -12 + 4 = -8...). Now, we can plug in the values of f(1) and 'd' to get the formula of this arithmetic sequence: f(n) = -20 + 4(n - 1).