Question

1. Consider the function f(x) = x^(n)e^(-2x) for x ≥ 0, where n is some unknown constant greater than 2.

A. Find the constant n for which the function f(x) attains its maximum value at x = 3. Make certain to justify that a maximum is attained.
B. For n = 4, find all x values of points of inflection for the curve y = f(x).

Answer 1

A. n = 6

B. x = 0, x = 1, x = 3

Step-by-step explanation:

Given function:

`f(x)=x^ne^(-2x),\;\;\; x\geq 0`

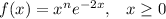
Part A

To find the constant n for which the function f(x) attains its maximum value at x = 3, first differentiate the function by using the product rule.

`\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

`\textsf{Let}\;u=x^n \implies \frac{\text{d}u}{\text{d}x}=nx^(n-1)`

`\textsf{Let}\;v=e^(-2x) \implies \frac{\text{d}v}{\text{d}x}=-2e^(-2x)`

Therefore, the derivative of function f(x) is:

`\begin{aligned}\implies f'(x)&=x^n\left(-2e^(-2x)\right)+e^(-2x)\left(nx^(n-1)\right)\\\\&=e^(-2x)\left(nx^(n-1)-2x^n\right)\end{aligned}`

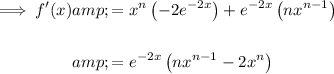
Set the derivative equal to zero:

`\begin{aligned}f'(x)&=0\\\implies e^(-2x)\left(nx^(n-1)-2x^n\right)&=0\\nx^(n-1)-2x^n&=0\end{aligned}`

Simplify:

`\begin{aligned}nx^(n-1)-2x^n&=0\\\implies nx^(n-1)-2x^(n-1+1)&=0\\nx^(n-1)-2x^(n-1)x^1&=0\\nx^(n-1)-2x \cdot x^(n-1)&=0\\x^(n-1)\left(n-2x\right)&=0\end{aligned}`

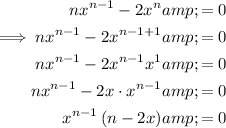
Substitute x = 3:

`\implies 3^(n-1)\left(n-6\right)=0`

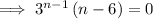
Use the Zero Factor principle to solve for n:

`3^(n-1)=0 \implies \textsf{No solution for $n \in \mathrm{R}$}`

`n-6=0 \implies n=6`

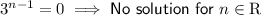
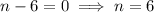
Therefore, the value of constant n for which the function f(x) attains its maximum value at x = 3 is n = 6.

To determine if this critical point is a maximum, we can use the second derivative test.

Differentiate f'(x) using the product rule.

`f'(x)=e^(-2x)\left(nx^(n-1)-2x^n\right)`

`\textsf{Let}\;u=e^(-2x) \implies \frac{\text{d}u}{\text{d}x}=-2e^(-2x)`

`\textsf{Let}\;v=nx^(n-1)-2x^n \implies \frac{\text{d}v}{\text{d}x}=(n-1)nx^(n-2)-2nx^(n-1)`

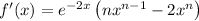
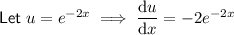
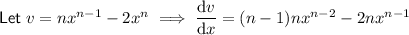
Therefore:

`\begin{aligned}f''(x)&=e^(-2x)\left((n-1)nx^(n-2)-2nx^(n-1)\right)-2e^(-2x)\left(nx^(n-1)-2x^n\right)\\&=e^(-2x)\left(n^2x^(n-2)-nx^(n-2)-2nx^(n-1)\right)-e^(-2x)\left(2nx^(n-1)-4x^n\right)\\&=e^(-2x)\left(n^2x^(n-2)-nx^(n-2)-2nx^(n-1)-2nx^(n-1)+4x^n\right)\\&=e^(-2x)\left(n^2x^(n-2)-nx^(n-2)-4nx^(n-1)+4x^n\right)\end{aligned}`

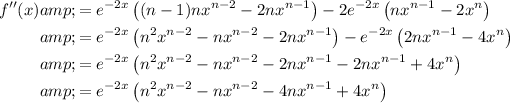
As n = 6:

`\begin{aligned}f''(x)&=e^(-2x)\left(6^2x^(6-2)-6x^(6-2)-4\cdot 6x^(6-1)+4x^6\right)\\&=e^(-2x)\left(36x^(4)-6x^(4)-24x^(5)+4x^6\right)\\&=e^(-2x)\left(4x^6-24x^5+30x^4\right)\end{aligned}`

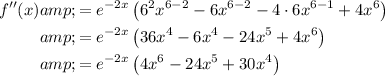
If f''(3) < 0, then x = 3 is a maximum. Substitute x = 3:

`\begin{aligned}\implies f''(3)&=e^(-2\cdot 3)\left(4\cdot 3^6-24\cdot 3^5+30 \cdot 3^4\right)\\&=e^(-6)\left(2916-5832+2430\right)\\&=-486e^(-6)\\&=-1.20467...\\\end{aligned}`

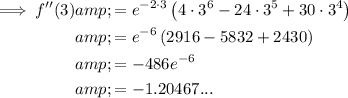
As f''(3) < 0, this justifies that a maximum is attained.

Part B

To find the points of inflection, we need to solve f''(x) = 0.

`f''(x)=e^(-2x)\left(n^2x^(n-2)-nx^(n-2)-4nx^(n-1)+4x^n\right)`

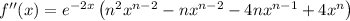
Therefore, when n = 4:

`\begin{aligned}f''(x)&=e^(-2x)\left(4^2x^(4-2)-4x^(4-2)-4\cdot 4x^(4-1)+4x^4\right)\\&=e^(-2x)\left(16x^(2)-4x^(2)-16x^(3)+4x^4\right)\\&=e^(-2x)\left(4x^4-16x^3+12x^2\right)\end{aligned}`

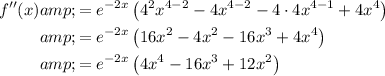
Set f''(x) equal to zero:

`\begin{aligned}f''(x)&=0\\\implies e^(-2x)\left(4x^4-16x^(3)+12x^(2)\right)&=0\\4x^4-16x^(3)+12x^(2)&=0\\4x^2(x^2-4x+3)&=0\end{aligned}`

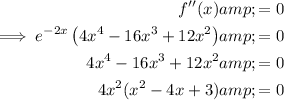
Use the Zero Factor principle to solve for x:

`\begin{aligned}4x^2&=0\\ \implies x&=0\\\\x^2-4x+3&=0\\x^2-3x-x+3&=0\\x(x-3)-1(x-3)&=0\\(x-1)(x-3)&=0\\\implies x&=1, 3\end{aligned}`

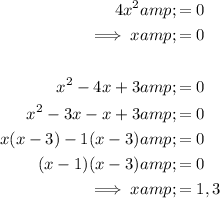
Therefore, the x-values of the points of inflection for the curve y = f(x) are:

• x = 0
• x = 1
• x = 3