Question

You're a contestant on a TV gameshow where you must choose between four identical looking suitcases containing $100, $100, $300, and $400. You start by randomly picking one suitcase. The host then opens the remaining suitcase with the lowest dollar amount. Now, you have the choice to keep your current suitcase or switch to one of the two remaining suitcases. With probability p= 0.7, you keep your original suitcase and open it. Otherwise, you are equally likely to choose either of two the remaining suitcases and open it. You win the money in the suitcase you opened.

Consider these events:
Ai is the event that the first suitcase you choose is worth i dollars.
Hi is the event that the host opens a suitcase worth i dollars.
Wi is the event that you win i dollars.

If you play this game five times, the probability that the event W400 occurs twice in five trials is:_______

Answer 1

0.2990 = 29.90%.

Explanation:

For each trial, there are only two possible outcomes. Either you win $400, or you do not. Trials are independent. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
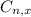`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

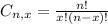
And p is the probability of X happening.

Probability of winning $400 in a trial:

1/4 probability of choosing the suitcase containing $400, and in this case, 0.7 probability of keeping it.

3/4 probability of choosing another suitcase. Then, 0.3 of 3/4 probability of changing the suitcase, and 0.5 of 0.3 of 3/4 probability of getting the suitcase containing $400. So

`p = (1)/(4)*0.7 + (3)/(4)*0.3*0.5 = 0.25*0.7 + 0.75*0.15 = 0.2875`

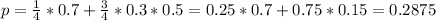
If you play this game five times, the probability that the event W400 occurs twice in five trials is:_______

This is P(X = 2) when n = 5. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(5,2).(0.2875)^(2).(0.7125)^(3) = 0.2990`

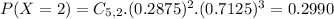
The probability is 0.2990 = 29.90%.