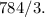Final Answer:
The value of the integral of
 over the triangular region cut from the first quadrant on the uv plane by the line
over the triangular region cut from the first quadrant on the uv plane by the line

Step-by-step explanation:
To solve this problem, we'll start by setting up the integral bounds. The line
 intersects the u and v axes at the points
intersects the u and v axes at the points
 and
and
 respectively, forming a triangle in the first quadrant. Integrating
respectively, forming a triangle in the first quadrant. Integrating
 over this triangular region involves breaking the integral into two parts: integrating with respect to v first and then u.
over this triangular region involves breaking the integral into two parts: integrating with respect to v first and then u.
For the inner integral with respect to v, the bounds are from 0 to
 as v varies from the line
as v varies from the line
 to the v-axis. The outer integral with respect to u ranges from 0 to 49, which are the limits of u within the triangular region.
to the v-axis. The outer integral with respect to u ranges from 0 to 49, which are the limits of u within the triangular region.
Now, performing the integration steps:

First, integrating with respect to \(v\) yields:
![\(\left[(v^2)/(2) - v√(u)\right]_(0)^(49-u) = \left(((49-u)^2)/(2) - (49-u)√(u)\right)\)](https://img.qammunity.org/2024/formulas/mathematics/high-school/r0mj6mtvtvnz0tcelc64cx715vlw3upb1o.png)
Then integrating this expression with respect to
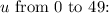
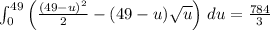
Therefore, the final answer to the integral over the triangular region is