Question

The radius of a sphere is increasing at a constant rate of 2 inches per minute. At the instant when the radius of the sphere is 9 9 inches, what is the rate of change of the volume? The volume of a sphere can be found with the equation � = 4 3 � � 3 . V= 3 4 ​ πr 3 . Round your answer to three decimal places.

Answer 1

2035.752 in³/min

Explanation:

To find the rate of change of the volume of the sphere at the instant its radius is 9 inches, we need to work out dV/dt when r = 9.

The equation for the volume of a sphere is:

`V=(4)/(3)\pi r^3`

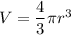
Differentiate the expression for volume with respect to r:

`\begin{aligned}V&=(4)/(3)\pi r^3\\\\\implies\frac{\text{d}V}{\text{d}r}&=3 \cdot (4)/(3) \pi r^(3-1)\\\\\frac{\text{d}V}{\text{d}r}&=4 \pi r^2\end{aligned}`

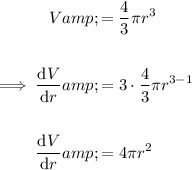
We know that that the radius of a sphere is increasing at a constant rate of 2 inches per minute, so the rate of change of the radius of sphere is:

`\frac{\text{d}r}{\text{d}t}=2`

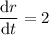
To find an expression for dV/dt, use the chain rule:

`\boxed{\frac{\text{d}V}{\text{d}t}=\frac{\text{d}V}{\text{d}r} * \frac{\text{d}r}{\text{d}t}}`

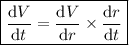
Substitute the expressions for dV/dr and dr/dt to create an expression for dV/dt:

`\begin{aligned}\implies \frac{\text{d}V}{\text{d}t}&=4 \pi r^2 * 2\\&=8 \pi r^2\end{aligned}`

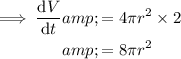
To find the value of dV/dt when r = 9, substitute r = 9 into the equation for dV/dt:

`\begin{aligned}\frac{\text{d}V}{\text{d}t}\;\textsf{at}\;r=9\implies \frac{\text{d}V}{\text{d}t}&=8 \pi (9)^2\\&=8\pi (81)\\&=648\pi\\&=2035.752\; \sf in^3/min\;(3\;d.p.)\end{aligned}`

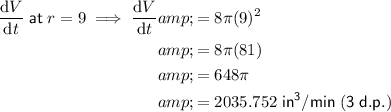
Therefore, the rate of change of the volume of the sphere at the instant when its radius is 9 inches is 2035.752 in³/min (rounded to three decimal places).