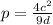Answer:
The relationship between d, c and p is that
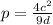
Explanation:
Roots of a quadratic equation:
The roots
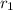 and
and
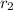 of a quadratic equation in the following format:
of a quadratic equation in the following format:

Can be given by:
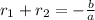
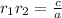
In this question:
We have the following quadratic equation:
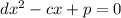
So
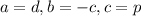
One of the roots is twice the other:
So
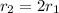
First relation:
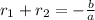
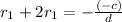
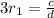
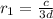
Second relation:
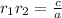

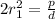
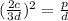

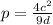
The relationship between d, c and p is that