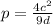Question

One of the root of the quadratic equation dx²-cx+p=0 is twice other. find the relationship between d, c, and p

please help...I don't understand atall​

Answer 1

The relationship between d, c and p is that
`p = (4c^2)/(9d)`

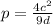
Explanation:

Roots of a quadratic equation:

The roots
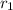`r_1` and
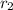`r_2` of a quadratic equation in the following format:

`ax^2 + bx + c = 0`

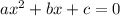
Can be given by:

`r_1 + r_2 = -(b)/(a)`

`r_1r_2 = (c)/(a)`

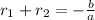
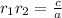
In this question:

We have the following quadratic equation:

`dx^2 - cx + p = 0`

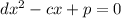
So
`a = d, b = -c, c = p`

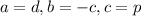
One of the roots is twice the other:

So
`r_2 = 2r_1`

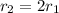
First relation:

`r_1 + r_2 = -(b)/(a)`

`r_1 + 2r_1 = -((-c))/(d)`

`3r_1 = (c)/(d)`

`r_1 = (c)/(3d)`

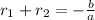
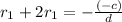
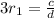
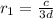
Second relation:

`r_1r_2 = (c)/(a)`

`r_1*2r_1 = (p)/(d)`

`2r_(1)^(2) = (p)/(d)`

`((2c)/(3d))^2 = (p)/(d)`

`(4c^2)/(9d^2) = (p)/(d)`

`p = (4c^2)/(9d)`

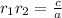
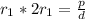
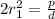
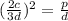
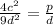
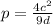
The relationship between d, c and p is that
`p = (4c^2)/(9d)`