Question

Given sinx=3/5 and is in quadrant 2, what is the value of tan x/2 ?

Answer 1

`\tan \left((x)/(2)\right)=3`

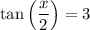
Explanation:

Trigonometric ratios are the ratios of the sides of a right triangle.

`\boxed{\begin{minipage}{9.4 cm}\underline{Trigonometric ratios} \\\\$\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

The sine trigonometric ratio is the ratio of the side opposite the angle to the hypotenuse.

Given sin(x) = 3/5, the side opposite angle x is 3, and the hypotenuse is 5.

As we have two sides of the right triangle, we can calculate the third side (the side adjacent the angle) using Pythagoras Theorem.

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

Therefore:

`\implies A^2+3^2=5^2`

`\implies A^2+9=25`

`\implies A^2+9-9=25-9`

`\implies A^2=16`

`\implies √(A^2)=√(16)`

`\implies A=4`

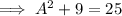
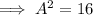
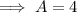
Use the cosine trigonometric ratio to find the value of cos(x), remembering that cosine is negative in Quadrant II.

`\implies \cos x=-(4)/(5)`

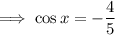
Now we have the values of sin(x) and cos(x) in Quadrant II, we can use the tangent half angle formula to find the value of tan(x/2).

`\begin{aligned}\implies \tan \left((x)/(2)\right)&=(\sin x)/(1+\cos x)\\\\&=((3)/(5))/(1-(4)/(5))\\\\&=((3)/(5))/((1)/(5))\\\\&=(3)/(5) \cdot (5)/(1)\\\\&=3\end{aligned}`

Therefore, the value of tan(x/2) is 3.