Answer:
The area will be:
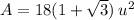 or
or
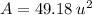 .
.
Explanation:
Using the definition of tangent, we have:

We know that tan(α) = 1, then we can find AB
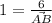

u means any unit.
Now, we need to find the distance BC. If the angle ∠D is 60°, then ∠C must be 30°. Using the tangent definition in the triangle BCD we have:
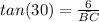
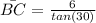
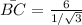
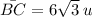
So, the base of the triangle will be:
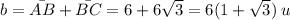
The area of a triangle is given by the following equation:
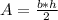
- b is the base (
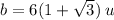 )
) - h is the height (h=6 u)
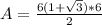
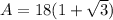
Therefore, the area will be
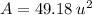 .
.
I hope it helps you!