Question

Given \cot A=\frac{3}{7}cotA= 7 3 ​ and that angle AA is in Quadrant I, find the exact value of \cos AcosA in simplest radical form using a rational denominator.

Answer 1

• 
  `\cos A =(3√(58))/(58)`

Explanation:

To find:-

• The value of cosA .

Answer:-

We are here given that , the value of ,

`\longrightarrow \cot A =(3)/(7)\\`

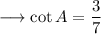
And we are interested in finding out the value of cos A is A is in first quadrant. For that as we know that , cotangent is defined as the ratio of base and perpendicular . That is ,

`\longrightarrow \cot A =(b)/(p) \\`

According to the question,

`\longrightarrow \cot A =(3)/(7)=(b)/(p) \\`

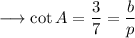
Let us take the given ratio to be 3x:7x .

Now again as we know that cosine is defined as the ratio of base and hypotenuse. So that ,

`\longrightarrow \cos A =(b)/(h) \\`

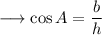
Now we don't know the value of hypotenuse. For that we can use the Pythagoras theorem .

Pythagoras theorem:-

• In a right angled triangle, the sum of squares of base and perpendicular is equal to the square of hypotenuse.

Mathematically,

`\longrightarrow p^2+b^2=h^2 \\`

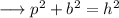
where the symbols have their usual meaning.

Now substitute the respective values to find out the value of hypotenuse as ,

`\longrightarrow (3x)^2+(7x)^2=h^2\\`

`\longrightarrow 9x^2+49x^2 = h^2 \\`

`\longrightarrow 58x^2 = h^2\\`

`\longrightarrow h =√(58x^2)\\`

`\longrightarrow \boldsymbol{ h = √(58)x }\\`

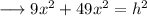
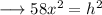
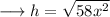
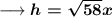
Now we can find the value of cosA as ,

`\longrightarrow \cos A =(b)/(h) \\`

`\longrightarrow \cos A = (3x)/(√(58)x)\\`

`\longrightarrow \cos A =(3)/(√(58)) \\`

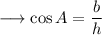
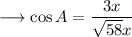
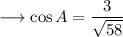
Rationalize the denominator by multiplying numerator and denominator by √58 as ,

`\longrightarrow \cos A =(3√(58))/(√(58)\cdot√(58))\\`

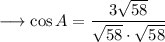
Simplify,

`\longrightarrow \boxed{\boldsymbol{\cos A =(3√(58))/(58)}} \\`

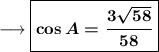
This is the required answer.