Question

Please answer the question

Answer 1

• 
  `x = 50\sqrt2`
• 
  `p = 141.4 \ ft`
• 
  `h = 424.2 \ ft`

Explanation:

To find:-

• The value of x .

Answer:-

Here we are given a right angled triangle with the side measures as , 2x , 6x and 400 ( unit is ft.) . To find out the value of "x" , we shall use Pythagoras theorem .

It is as follows,

Pythagoras theorem :-

• In a right angled triangle , the sum of squares of base and perpendicular is equal to the square of hypotenuse.

Mathematically, if
`p` is the perpendicular ,
`b` is the base, and
`h` is the hypotenuse, then ;

`\longrightarrow p^2+b^2=h^2\\`

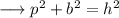
From the given triangle, we can see that,

• perpendicular = 2x
• base = 400
• hypotenuse = 6x

On substituting the respective values, we have;

`\longrightarrow (2x)^2 + (400)^2 = (6x)^2 \\`

`\longrightarrow 4x^2 + 160000 = 36x^2 \\`

`\longrightarrow 36x^2-4x^2=160000 \\`

`\longrightarrow 32x^2 = 160000\\`

`\longrightarrow x^2=(160000)/(32) \\`

`\longrightarrow x^2 = 5000 \\`

`\longrightarrow x =√(5* 10^3)\\`

`\longrightarrow x =√( 5 (10)^2(5)(2)) \\`

`\longrightarrow x = 10(5)√(2)\\`

`\longrightarrow \red{ x = 50\sqrt2} \\`

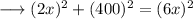
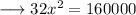
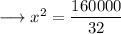
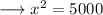
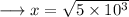
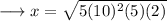
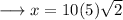
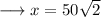
Hence the value of x is 50√2 .

To find out the values of the sides , plug in the value of x in the given expressions for the sides as ,

`\longrightarrow p = 2x \\`

`\longrightarrow p =2(50\sqrt2)\\`

`\longrightarrow p = 100\sqrt2 = 100* 1.414\\`

`\longrightarrow \boxed{ p = 141.4 \ ft.} \\`

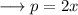
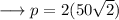
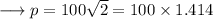
Similarly,

`\longrightarrow h = 6x = 6(50\sqrt2) \\`

`\longrightarrow h = 300\sqrt2 = 300(1.414)\\`

`\longrightarrow \boxed{ h = 424.2 \ ft } \\`

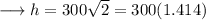
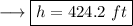
This is the required answer.

Answer 2

`x = 50√(2)`

`\textsf{Leg\;$2x$}=141.4\; \sf ft\;(nearest\;tenth)`

`\textsf{Hypotenuse\;$6x$}=424.3\; \sf ft\;(nearest\;tenth)`

Explanation:

To solve the given problem, use Pythagoras Theorem.

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

From inspection of the given right triangle:

• 
  `a = 2x`
• 
  `b = 400`
• 
  `c = 6x`

Substitute the values of a, b and c into the formula and solve for x:

`\implies (2x)^2+400^2=(6x)^2`

`\implies 4x^2+160000=36x^2`

`\implies 4x^2+160000-4x^2=36x^2-4x^2`

`\implies 160000=32x^2`

`\implies 32x^2=160000`

`\implies (32x^2)/(32)=(160000)/(32)`

`\implies x^2=5000`

`\implies √(x^2)}=√(5000)`

`\implies x=√(5000)`

`\implies x=√(2500 \cdot 2)`

`\implies x=√(2500)√(2)`

`\implies x=50√(2)`

Therefore, the value of x is 50√2.

To find the measures of the side lengths, substitute the found value of x into the expression for each side.

`\begin{aligned}\textsf{Leg\;$2x$}&=2 \cdot 50 √(2)\\&=100√(2)\\&=141.421356...\\&=141.4\; \sf ft\;(nearest\;tenth)\end{aligned}`

`\begin{aligned}\textsf{Hypotenuse\;$6x$}&=6 \cdot 50 √(2)\\&=300√(2)\\&=424.264068...\\&=424.3\; \sf ft\;(nearest\;tenth)\end{aligned}`

Therefore, the side lengths of the given right triangle to the nearest tenth are:

• 400 ft
• 141.4 ft
• 424.3 ft