Answer:
Explanation:
To find:-
Answer:-
Here we are given a right angled triangle with the side measures as , 2x , 6x and 400 ( unit is ft.) . To find out the value of "x" , we shall use Pythagoras theorem .
It is as follows,
Pythagoras theorem :-
- In a right angled triangle , the sum of squares of base and perpendicular is equal to the square of hypotenuse.
Mathematically, if
 is the perpendicular ,
is the perpendicular ,
 is the base, and
is the base, and
 is the hypotenuse, then ;
is the hypotenuse, then ;
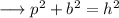
From the given triangle, we can see that,
- perpendicular = 2x
- base = 400
- hypotenuse = 6x
On substituting the respective values, we have;
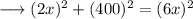
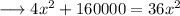
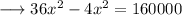
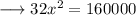
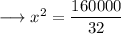
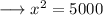
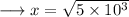
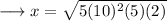
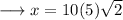
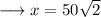
Hence the value of x is 50√2 .
To find out the values of the sides , plug in the value of x in the given expressions for the sides as ,
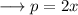
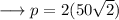
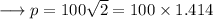
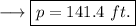
Similarly,
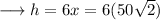
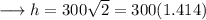
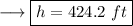
This is the required answer.