Question

Consider the quadratic function f(x) = x2 – 5x + 12. Which statements are true about the function and its graph? Select three options. The value of f(–10) = 82 The graph of the function is a parabola. The graph of the function opens down. The graph contains the point (20, –8). The graph contains the point (0, 0).

Answer 1

The statements that are true about the function and its graph are:

The graph of the function is a parabola.

The graph contains the point (0,0).

The graph does not contain the point (20,-8).

Step-by-step explanation:

The function f(x) = x^2 - 5x + 12 is a quadratic function, which means its graph is a parabola.

To find out whether the graph contains the point (0,0), we can check if f(0) = 0. Substituting x = 0 into the function, we get f(0) = 0^2 - 5(0) + 12 = 12. Since f(0) is not equal to 0, the point (0,0) is not on the graph.

To find out whether the graph contains the point (20,-8), we can check if f(20) = -8. Substituting x = 20 into the function, we get f(20) = 20^2 - 5(20) + 12 = 232. Since f(20) is not equal to -8, the point (20,-8) is not on the graph.

Answer 2

The true statements about the function and its graph are:

• The value of f(-10) = 82.
• The graph of the function is a parabola.
• The graph contains the point (20, -8).

Step-by-step explanation:

Given quadratic function:

`f(x) = (1)/(5)x^2 - 5x + 12`

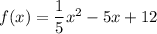
When a quadratic function is graphed on the coordinate plane, the function forms a curve called a parabola.

If the leading co-efficient of the quadratic function is positive, the parabola opens upwards. If the leading co-efficient is negative, the parabola opens downwards.

As the leading co-efficient of the given quadratic function is positive, the parabola opens upwards.

To find the value of f(-10), substitute x = -10 into the function:

`\begin{aligned}f(-10)&=(1)/(5)(-10)^2-5(-10)+12\\&=20+50+12\\&=70+12\\&=82\end{aligned}`

Therefore, f(-10) = 82.

To determine if the graph contains the point (20, -8), substitute x = 20 into the function:

`\begin{aligned}f(20)&=(1)/(5)(20)^2-5(20)+12\\&=80-100+12\\&=-20+12\\&=-8\end{aligned}`

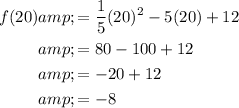
Therefore, the graph contains the point (20, -8).

To determine if the graph contains the point (0, 0), substitute x = 0 into the function:

`\begin{aligned}f(0)&=(1)/(5)(0)^2-5(0)+12\\&=0-0+12\\&=0+12\\&=12\end{aligned}`

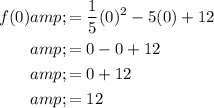
Therefore, the graph contains the point (0, 12), not point (0, 0).

The true statements about the function and its graph are:

• The value of f(-10) = 82.
• The graph of the function is a parabola.
• The graph contains the point (20, -8).