Answer:

Explanation:
Since we are given the central angle in radians, we should use this formula for the sector area:
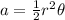
where r is the radius and θ is the angle in radians.
The radius is 14 units and the angle is 7.2 radians.
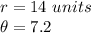
Substitute the values into the formula.
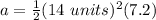
Solve the exponent.
- (14 units)²= 14 units* 14 units =196 units²
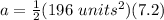
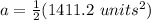
Multiply by 1/2 or divide by 2.
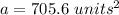
The area of the sector is 705.6 square units.