Question

Find the area of a sector with a central angle of 7.2 radians and a radius of 14 units

Please include steps

Answer 1

`\boxed {\boxed {\sf a= 705.6 \ units^2 }}`

Explanation:

Since we are given the central angle in radians, we should use this formula for the sector area:

`a=(1)/(2)r^2 \theta`

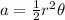
where r is the radius and θ is the angle in radians.

The radius is 14 units and the angle is 7.2 radians.

`r= 14 \ units \\\theta= 7.2`

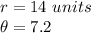
Substitute the values into the formula.

`a= (1)/(2) (14 \ units)^2 (7.2)`

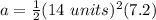
Solve the exponent.

• (14 units)²= 14 units* 14 units =196 units²

`a=( 1)/(2) (196 \ units^2)(7.2)`

`a=( 1)/(2)(1411.2 \ units^2)`

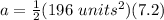
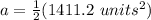
Multiply by 1/2 or divide by 2.

`a= 705.6 \ units^2`

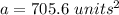
The area of the sector is 705.6 square units.