Question

Which expression represents the same solution as (4)(-3 1/8)?

(4)(-3)+(4)(1/8)
(4)(-3)+(4)(-1/8)
(4+-3)x(4+1/8)
(4+-3)x(4+-1/8)

Answer 1

Option B.

Explanation:

`\left(4\right)\left(-3(1)/(8)\right) = \left(4\right)\left\left(-(25)/(8)\right)`

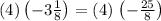
Next, remove the brackets.

`=4\left(-(25)/(8)\right)\\=-4* (25)/(8)`

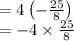
Then, convert 4 into a fraction.

`=-4* (25)/(8)\\=-(4* 25)/(1* 8)`

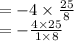
Multiply the bottom numbers then factor.

`=-(4* 25)/(8)\\=-(4* 25)/(4* 2)`

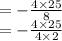
Now, in order to continue, you have to cancel the common factor, 4.

`=-(25)/(2)\\= -12(1)/(2)`

Why option B is the same as the original equation is because it's the same equation with more steps.

Option B:

`\left(4\right)\left(-3\right)+\left(4\right)\left(-1/8\right) = (-1)/(8)\\=\left(4\right)\left(-3\right)+\left(4\right)(-1)/(8)\\\left(4\right)\left(-3\right) = -12\\=-12+\left(4\right)(-1)/(8)\\\left(4\right)(-1)/(8) = 4\left(-(1)/(8)\right)\\= -(4)/(1)* (1)/(8)\\=-(4* 1)/(1* \:8)\\= -(4)/(8)\\=-(1)/(2)\\=-12-(1)/(2)\\=-(25)/(2)`

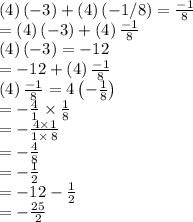
And 25 halves is 12 and a half, so this is why option B is identical.

Hope this helps!