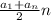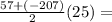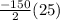Answer:
-1875
Explanation:
An arithmetic sequence has a common difference as a sequence. Here the common differnece is -11.
So our sequence so far looks like,
(57,46,35,24....). We know the last term of the sequence is -207 and we need to find the nth term of that series so we use arithmetic sequence
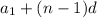
where a1 is the inital value,
d is the common differnece and n is the nth term.
We need to find the nth term so
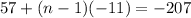
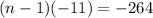
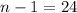

So the 25th term of a arithmetic sequence is last term, now we can use the sum of arithmetic sequence
which is