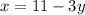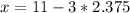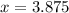Answer:
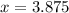

Explanation:
See comment for complete question.
Given
A.
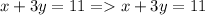


B.
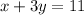

Required
Determine the values of x and y
The first equation in B is:
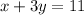
In (a): 5x - y = 17 is multiplied by 3, then added to x + 3y = 11.
So, the second equation is:
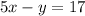
Solving (a) & (b):
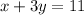 --- (1)
--- (1)
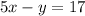 ---- (2)
---- (2)
Make x the subject in (1)
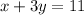
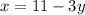
Substitute
 for x in
for x in
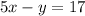
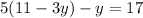
Open bracket
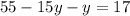
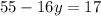
Collect Like Terms
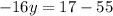
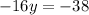
Solve for y
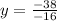
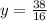

Substitute 2.375 for y in