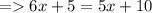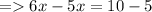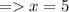Answer:
x = 5
Explanation:
__________________________________________________________
FACTS TO KNOW BEFORE SOLVING :-
- In an equation , if the bases are same in both L.H.S. & R.H.S. then , the power of the bases on both the sides of equation should be equal. For e.g. :
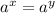 ⇒
⇒
 [∵ Bases are equal on both the sides]
[∵ Bases are equal on both the sides]
__________________________________________________________
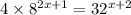
Lets express it in terms of 2.
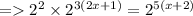
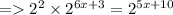
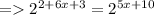
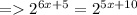
Here the bases on both the sides are equal. Hence ,