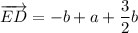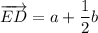Question

In the diagram, BCE and ACD are straight lines. AB =2a and

BC= 3b. The point C divides AD in the ratio 2 : 1 and divides BE
in the ratio 3: 1. Express in terms of a and b, the vectors:
(a) AC->
(c) CE->
(b) CD->
(d) ED->

Answer 1

`\textsf{a)}\quad \overrightarrow{AC}=2a+3b`

`\textsf{b)}\quad \overrightarrow{CE}=b`

`\textsf{c)}\quad \overrightarrow{CD}=a+(3)/(2)b`

`\textsf{d)}\quad \overrightarrow{ED}=a+(1)/(2)b`

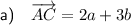
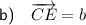
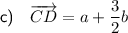
Explanation:

Part (a)

To find vector AC, we can add vectors AB and BC.

`\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}`

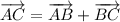
Given that AB = 2a and BC = 3b, then:

`\overrightarrow{AC}=2a+3b`

`\hrulefill`

Part (b)

If point C divides BE in the rato 3 : 1, then:

`\overrightarrow{BC}:\overrightarrow{CE}=3:1`

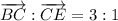
Given that BC = 3b, then:

`3b:\overrightarrow{CE}=3:1`

`\overrightarrow{CE}=b`

`\hrulefill`

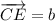
Part (c)

If point C divides AD in the rato 2 : 1, then:

`\overrightarrow{AC}:\overrightarrow{CD}=2:1`

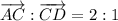
Given that AC = 2a + 3b from part (a), then:

`\overrightarrow{2a+3b}:\overrightarrow{CD}=2:1`

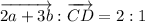
Therefore:

`\overrightarrow{CD}=(2a+3b)/(2)`

`\overrightarrow{CD}=a+(3)/(2)b`

`\hrulefill`

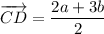
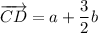
Part (d)

To find vector ED, we can add vectors EC and CD:

`\overrightarrow{ED}=\overrightarrow{EC}+\overrightarrow{CD}`

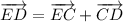
Substituting CD = a + ³/₂b from part (c) givens:

`\overrightarrow{ED}=\overrightarrow{EC}+a+(3)/(2)b`

Given that CE = b, then EC = -b. Therefore:

`\overrightarrow{ED}=-b+a+(3)/(2)b`

`\overrightarrow{ED}=a+(1)/(2)b`

Answer 2

`\sf \overrightarrow{AC } = 2a+3b`

`\sf \overrightarrow{CE } = b`

`\sf \overrightarrow{CD } = a + (3b)/(2)`

`\sf \overrightarrow{ED} = a + (1)/(2)b`

Explanation:

Given:

• BCE and ACD are straight lines.
• 
  `\sf \overrightarrow{AB } = 2a`
• 
  `\sf \overrightarrow{BC } = 3b`
• The point C divides AD in the ratio 2 : 1 and divides B in the ratio 3: 1.

To find:

• 
  `\sf \overrightarrow{AC } = ?`
• 
  `\sf \overrightarrow{CE } = ?`
• 
  `\sf \overrightarrow{CD } = ?`
• 
  `\sf \overrightarrow{ED} = ?`

Solution:

We can use the Triangle Law of the vector to find the magnitude and direction of the resultant vector.

Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.

Thus, we get

`\sf \overrightarrow{AC } = \overrightarrow{AB }+ \overrightarrow{BC }`

`\sf \overrightarrow{AC } = 2a+3b`

`\sf \hrulefill`

it is given that

`\sf \frac{ \overrightarrow{BC }} {\overrightarrow{CE }} =(3)/(1)`

`\sf \frac{ \overrightarrow{3b }} {\overrightarrow{CE }} =(3)/(1)`

`\sf \overline{CE }=(3b)/(3)`

`\sf \overrightarrow{CE } = b`

`\sf \hrulefill`

It is given that
`\sf \overrightarrow{AC }:\overrightarrow{CD } = 2:1`

`\sf \frac{ \overrightarrow{AC } } {\overrightarrow{CD }} =(2)/(1)`

`\sf \frac{ 2a +3b } {\overrightarrow{CD }} =(2)/(1)`

`\sf \overrightarrow{CD } =( 2a + 3b)/(2)`

`\sf \overrightarrow{CD } = a + (3b)/(2)`

`\sf \hrulefill`

Now, consider ∆CED, and apply the triangle law of addition of two vectors, we get

`\sf \overrightarrow{ED} = \overrightarrow{EC} + \overrightarrow{CD}`

`\sf \overrightarrow{ED} = -b + a + (3b)/(2)`

`\sf \overrightarrow{ED} = a + (-2b +3b)/(2)`

`\sf \overrightarrow{ED} = a + (1)/(2)b`

Summary:

`\sf \overrightarrow{AC } = 2a+3b`

`\sf \overrightarrow{CE } = b`

`\sf \overrightarrow{CD } = a + (3b)/(2)`

`\sf \overrightarrow{ED} = a + (1)/(2)b`