Question

A box of books weighing 315 N is shoved across the floor by a force of 477 N exerted downward at an angle of 35° below the horizontal. If the coefficient of kinetic friction between the box and the floor is 0.58, how long does it take to move the box 4.20 m starting from rest?

Answer 1

It takes 1.14 s to move the box 4.20 m.

Step-by-step explanation:

Using Newton's second law we have:

`Fcos(35)-F_(f)=ma`

`Fcos(35)-\mu mg=ma`

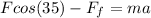
F is the force exerted and m the mass of the books

`Fcos(35)-\mu mg=ma`

`477cos(35)-(0.58*315)=(315)/(9.81)a`

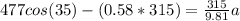
So, the books accelerate at:

`a=6.48\: m/s^(2)`

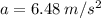
We know that the initial velocity is zero, so using the kinematic position equation, we have:

`x=(1)/(2)at^(2)`

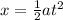
So, we just need to solve the equation for t.

`4.2=(1)/(2)6.48t^(2)`

`t=\sqrt{(2*4.2)/(6.48)}`

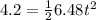
Taking the positive value of t:

`t=1.14\: s`

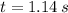
Therefore, it takes 1.14 s to move the box 4.20 m.

I hope it helps you!