Answer:
Se requiere una fuerza de 854.473 newtons sobre el émbolo pequeño.
Explanation:
Por el Principio de Pascal se conoce que el esfuerzo experimentado por el elefante es igual a la presión ejercida por el plato pequeño. Es decir:
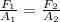 (1)
(1)
Donde:
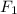 - Fuerza experimentada por el elefante, medida en newtons.
- Fuerza experimentada por el elefante, medida en newtons.
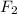 - Fuerza aplicada sobre el plato pequeño, medida en newtons.
- Fuerza aplicada sobre el plato pequeño, medida en newtons.
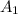 - Área del plato grande, medida en metros cuadrados.
- Área del plato grande, medida en metros cuadrados.
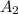 - Área del plato pequeño, medida en metros cuadrados.
- Área del plato pequeño, medida en metros cuadrados.
La fuerza aplicada sobre el plato pequeño es:
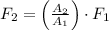
La fuerza experimentada por el elefante es su propio peso. Por otra parte, el área del plato es directamente proporcional al cuadrado de su diámetro. Es decir:
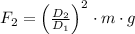 (2)
(2)
Donde:
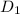 - Diámetro del plato grande, medido en centímetros.
- Diámetro del plato grande, medido en centímetros.
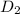 - Diámetro del plato pequeño, medido en centímetros.
- Diámetro del plato pequeño, medido en centímetros.
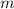 - Masa del elefante, medida en kilogramos.
- Masa del elefante, medida en kilogramos.
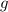 - Aceleración gravitacional, medida en metros por segundo cuadrado.
- Aceleración gravitacional, medida en metros por segundo cuadrado.
Si sabemos que
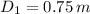 ,
,
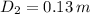 ,
,
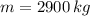 y
y
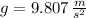 , entonces la fuerza a aplicar al émbolo pequeño es:
, entonces la fuerza a aplicar al émbolo pequeño es:
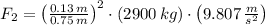
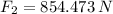
Se requiere una fuerza de 854.473 newtons sobre el émbolo pequeño.