Question

A leading magazine (like Barron's) reported at one time that the average number of weeks an individual is unemployed is 30 weeks. Assume that for the population of all unemployed individuals the population mean length of unemployment is 30 weeks and that the population standard deviation is 2.8 weeks. Suppose you would like to select a random sample of 56 unemployed individuals for a follow-up study.

Required:
a. Find the probability that a single randomly selected value is greater than 27.6.
b. Find the probability that a sample of size n=80 is randomly selected with a mean greater than 27.6.

Answer 1

a) The probability that a single randomly selected value is greater than 27.6

P( X≥27.6) = 0.8051

b) The probability that a sample of size randomly selected value is greater mean greater than 27.6

P( X≥27.6) = 0.9998

Explanation:

Step(i):-

Given that the mean of the Population = 30 weeks

The Standard deviation of the Population = 2.8 weeks

Let 'X' be a Normal distribution

`Z = (x-mean)/(S.D) = (27.6-30)/(2.8) = -0.857`

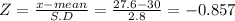
The probability that a single randomly selected value is greater than 27.6

P( X≥27.6) = P(Z≥-0.857)

= 0.5 + A(-0.857)

= 0.5 + A(0.857)

= 0.5 + 0.3051

= 0.8051

Step(ii):-

Let 'X' be a Normal distribution

`Z = (x^(-) -mean)/((S.D)/(√(n) ) ) = (27.6-30)/((2.8)/(√(80) ) ) = -7.6677`

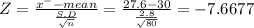
The probability that a sample of size randomly selected value is greater mean greater than 27.6

P( X≥27.6) = P(Z≥-7667)

= 0.5 + A(-7.667)

=0.5 +0.4998

= 0.9998