Answer:
a) The probability that a single randomly selected value is greater than 27.6
P( X≥27.6) = 0.8051
b) The probability that a sample of size randomly selected value is greater mean greater than 27.6
P( X≥27.6) = 0.9998
Explanation:
Step(i):-
Given that the mean of the Population = 30 weeks
The Standard deviation of the Population = 2.8 weeks
Let 'X' be a Normal distribution
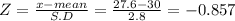
The probability that a single randomly selected value is greater than 27.6
P( X≥27.6) = P(Z≥-0.857)
= 0.5 + A(-0.857)
= 0.5 + A(0.857)
= 0.5 + 0.3051
= 0.8051
Step(ii):-
Let 'X' be a Normal distribution
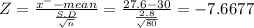
The probability that a sample of size randomly selected value is greater mean greater than 27.6
P( X≥27.6) = P(Z≥-7667)
= 0.5 + A(-7.667)
=0.5 +0.4998
= 0.9998