The new angular velocity of the combined system, after a smaller disk is dropped onto a larger rotating disk, is
 times the initial angular velocity of the larger disk.
times the initial angular velocity of the larger disk.
To find the new angular velocity of the combined system after the second disk is dropped onto the rotating disk, we can use the principle of conservation of angular momentum.
The angular momentum
 of an object is given by the product of its moment of inertia
of an object is given by the product of its moment of inertia
 and angular velocity
and angular velocity

![\[L = I \omega\]](https://img.qammunity.org/2024/formulas/physics/high-school/1le8nl60w4ou683h12rk4szp9c0v6a7euc.png)
The moment of inertia of a uniform disk rotating about its center is given by the expression
 where
where
 is the mass of the disk and
is the mass of the disk and
 is the radius.
is the radius.
The conservation of angular momentum states that the total angular momentum of an isolated system remains constant unless acted upon by an external torque.
Initially, the first disk is rotating with an angular velocity
 and has an angular momentum
and has an angular momentum
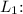
![\[L_1 = I_1 \omega_0 = (1)/(2) m r^2 \omega_0\]](https://img.qammunity.org/2024/formulas/physics/high-school/qhs51vsjhb51zi5hi7q1nf3d9gwzfd9168.png)
When the second disk is dropped onto the first one, the moment of inertia of the system becomes the sum of the individual moments of inertia:
![\[I_{\text{total}} = I_1 + I_2 = (1)/(2) m r^2 + (1)/(2) m \left((r)/(2)\right)^2 = (5)/(8) m r^2\]](https://img.qammunity.org/2024/formulas/physics/high-school/kk8ub4fcs3azs3vw8jv3gvz70ueltymday.png)
Let
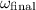 be the final angular velocity of the combined system. The final angular momentum
be the final angular velocity of the combined system. The final angular momentum
 is given by:
is given by:
![\[L_{\text{final}} = I_{\text{total}} \omega_{\text{final}}\]](https://img.qammunity.org/2024/formulas/physics/high-school/onr7h4yp3tye5theo3bsavjvky26lqg38z.png)
Since angular momentum is conserved,
 must be equal to
must be equal to
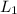 initially:
initially:
![\[(1)/(2) m r^2 \omega_0 = (5)/(8) m r^2 \omega_{\text{final}}\]](https://img.qammunity.org/2024/formulas/physics/high-school/co9qyhv2ufiq7uogm9qvt4xxqgzf3jrj4b.png)
Solving for
 we get:
we get:
![\[\omega_{\text{final}} = (1)/(5) \omega_0\]](https://img.qammunity.org/2024/formulas/physics/high-school/70glh6c82lsrt363paqqi6vo557inff1qd.png)
So, the new angular velocity of the combined system is
 times the initial angular velocity of the first disk.
times the initial angular velocity of the first disk.