Question

It can be shown that the function g(x)={ 10

​∣x∣<1
∣x∣>1​ has the following Fourier Integral Representation: g(x)= π2​ ∫ 0[infinity]​ wsin(w)​ cos(wx)dw(B(w)=0, of course). Use the above to find the Fourier Integral Representation of the function f(x)= xsin(x)

Answer 1

To find the Fourier Integral Representation of the function f(x) = xsin(x), substitute the expression into the given representation of g(x) and solve for f(x).

Step-by-step explanation:

To find the Fourier Integral Representation of the function f(x) = xsin(x), we can use the given representation of the function
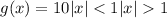`g(x) = 10 |x| < 1 |x| > 1`e f(x) in terms of g(x) by setting x = w, resulting in f(w) = wsin(w). We can then substitute this expression into the given Fourier Integral Representation of g(x) to find the representation of f(x).

Thus, the Fourier Integral Representation of the function f(x) = xsin(x) is:

`f(x) = π2 ∫0∞ wsin(w)cos(wx)dw`

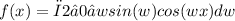
(B(w) = 0, of course)