Question

Let A be some constant and consider the function F(x)=ln(1+x)−

1+x/Ax for x>−1. Determine the global minimum of F.

Answer 1

To find the global minimum of the function F(x)=ln(1+x)−1+x/Ax, we need to find the critical points of the function by setting the first derivative equal to zero and solving for x. The second derivative is then used to determine whether these critical points correspond to a global minimum or maximum.

Step-by-step explanation:

To find the global minimum of the function F(x) = ln(1+x) - 1+x/Ax, we need to find the critical points of the function. The critical points occur where the derivative of the function is equal to zero. Differentiating the function with respect to x, we get:


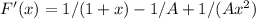`F'(x) = 1/(1+x) - 1/A + 1/(Ax^2)` solving for x, we find:

1/(1+x) - 1/A + 1/(Ax^2) = 0

Multiplying through by (1+x)(Ax^2), we get:

Ax^2 - 1 + (1+x) = 0

Simplifying the equation, we have:

Ax^2 + Ax - 1 = 0

Using the quadratic formula, we can solve for x in terms of A:

x = (-A ± sqrt(A^2 + 4A))/(2A)

Now, to determine whether these critical points correspond to a global minimum or maximum, we need to analyze the second derivative of the function. Differentiating F'(x) with respect to x, we get:

F''(x) = -1/(1+x)^2 - 2/(Ax^3)